WAEC SSCE - Physics - 2019
Ibeere 1 Ìròyìn
Which of the following statements is the correct reason for using soft iron in making the armature or an electric bell?
Awọn alaye Idahun
Ibeere 2 Ìròyìn
Which of the following materials does not serve as a safety device in electrical circuits?
Awọn alaye Idahun
Connecting wires, earth wires, and fuses serve as safety devices in electrical circuits, while switches are not safety devices but rather control devices that allow the flow of current to be turned on or off. Therefore, the correct answer is switch.
Ibeere 3 Ìròyìn
Calculate the quantity of heat needed to change the temperature of 60g of ice at 0 °C to 80 °C. [specific latent heat of fusion of ice= 3.36 x 10\(^5\) Jkg\(^{-1}\) specific heat capacity of water 4.2 x 10\(^3\) J kg\(^{-1}\) K\(^{-1}\)]
Awọn alaye Idahun
The heat needed to change the temperature of 60g of ice at 0°C to 80°C can be calculated using the equation for heat transfer: Q = m * c * ΔT Where Q is the heat transferred, m is the mass of the substance, c is the specific heat capacity of the substance, and ΔT is the change in temperature. First, the heat needed to melt the ice can be calculated using the specific latent heat of fusion: Qfusion = m * Lf Where Lf is the specific latent heat of fusion. Qfusion = 60g * 3.36 x 10^5 J/kg = 2.016 x 10^5 J Next, the heat needed to raise the temperature of the water from 0°C to 80°C can be calculated using the specific heat capacity of water: Qheat = m * c * ΔT Qheat = 60g * 4.2 x 10^3 J/kg/K * 80°C = 2.016 x 10^5 J The total heat needed to change the temperature of the ice to 80°C is the sum of the heat needed to melt the ice and the heat needed to raise the temperature of the water: Q = Qfusion + Qheat = 2.016 x 10^5 J + 2.016 x 10^5 J = 4.032 x 10^5 J = 40.32 kJ Therefore, the quantity of heat needed to change the temperature of 60g of ice at 0°C to 80°C is 40.32 kJ.
Ibeere 4 Ìròyìn
The area under a velocity-time graph represents
Awọn alaye Idahun
The area under a velocity-time graph represents the distance traveled by an object. Velocity is the rate of change of displacement with respect to time, which means it indicates how far an object has traveled in a specific amount of time. The area under the velocity-time graph shows the product of velocity and time, which is distance. To calculate the distance traveled, we need to find the area enclosed by the velocity-time graph, which may consist of different shapes depending on the motion of the object. For example, if the object is moving at a constant velocity, the area would be a rectangle. If the object is accelerating, the area would be a triangle or a trapezoid. Therefore, the correct answer is "distance".
Ibeere 5 Ìròyìn
The graph above illustrates the variation of temperature \(\theta\) with time (t) for a solid that is being heated. Which processes take place at segments P and Q respectively?
Awọn alaye Idahun
The graph shows the change in temperature of a solid as it is heated over time. At segment P, the temperature remains constant despite the application of heat. This is because the energy is being used to break the bonds between the molecules in the solid, rather than increasing their kinetic energy and temperature. This process is called melting, which is the transition from solid to liquid phase. At segment Q, the temperature again remains constant, but this time at a higher level than at segment P. This is because the energy is being used to break the bonds between the molecules in the liquid, rather than increasing their kinetic energy and temperature. This process is called boiling, which is the transition from liquid to gas phase. Therefore, the correct answer is "Melting and boiling".
Ibeere 6 Ìròyìn
An 800 kg car moving at 80 km hr\(^{-1}\) collides with a 1200 kg car moving at 40 km hr\(^{-1}\) in the same direction. If the cars stick together, calculate their common velocity.
Awọn alaye Idahun
Ibeere 7 Ìròyìn
The nucleon and proton numbers of a neutral atom of an element are 238 and 92 respectively. Determine the number of neutrons in the atom.
Awọn alaye Idahun
The nucleon number of an atom is the total number of protons and neutrons in its nucleus, while the proton number is the number of protons. Therefore, to determine the number of neutrons in an atom, we can subtract the proton number from the nucleon number. In this case, the nucleon number is 238 and the proton number is 92. Number of neutrons = Nucleon number - Proton number Number of neutrons = 238 - 92 Number of neutrons = 146 Therefore, the answer is: 146 neutrons.
Ibeere 8 Ìròyìn
A loaded spring is set in simple harmonic motion. The force that tends to restore the load to its equilibrium position is
Awọn alaye Idahun
Ibeere 9 Ìròyìn
Which of the following instruments can be used to compare the magnitudes of charges on two given bodies?
Awọn alaye Idahun
The instrument that can be used to compare the magnitudes of charges on two given bodies is the Gold-leaf electroscope. When a charged object is brought close to the electroscope, the charge is transferred to the metal leaves causing them to repel each other. By comparing the extent of separation of the leaves with a known charge, the magnitude of the charge on the given bodies can be determined. Electrophorus and ebonite rods are used for charging objects, and proof planes are used to transfer charge from one body to another.
Ibeere 11 Ìròyìn
Which of the following quantities is a vector?
Awọn alaye Idahun
Out of the given options, the quantity that is a vector is momentum. A vector quantity has both magnitude and direction. Momentum is the product of mass and velocity, and it has both magnitude and direction. On the other hand, volume, energy, and speed are scalar quantities that have only magnitude but no direction associated with them.
Ibeere 12 Ìròyìn
The wire of a platinum resistance thermometer has d resistance of 3.5\(\Omega\) at 0 °C and 10.52\(\Omega\) at 100°C. Calculate the temperature of the wire when its resistance is 7.5\(\Omega\).
Awọn alaye Idahun
The resistance (R) of a wire is proportional to the temperature (T) in degrees Celsius. The equation of the resistance-temperature relationship is given by: R = R0 (1 + αT) Where R0 is the resistance at 0°C, α is the temperature coefficient of resistance and T is the temperature in degrees Celsius. To solve this problem, we can use the resistance-temperature relationship to find α, and then use it to find the temperature at the given resistance. First, we need to find the value of α. We can use the two resistance values given to set up two equations: R1 = R0 (1 + αT1) R2 = R0 (1 + αT2) where R1 and R2 are the resistances at temperatures T1 and T2, respectively. Substituting the given values: 3.5 = R0 (1 + α(0)) 10.52 = R0 (1 + α(100)) Solving for R0: 3.5 = R0 1 + α(100) = 10.52/R0 Rearranging the second equation: α = (10.52/R0 - 1)/100 Substituting R0 = 3.5: α = (10.52/3.5 - 1)/100 = 0.0032/°C Now we can use the resistance-temperature relationship to find the temperature at the given resistance: R = R0 (1 + αT) 7.5 = 3.5 (1 + 0.0032T) Solving for T: T = (7.5/3.5 - 1)/0.0032 = 57°C Therefore, the temperature of the wire when its resistance is 7.5Ω is 57°C. The correct option is 57 \(^o\)C.
Ibeere 13 Ìròyìn
Two bodies of masses 3.0 kg and 2.0 kg are separated by a distance of 50 cm. Calculate the force of attraction between them. [G = 6.67 x 10\(^{-11}\) Nm\(^2\) kg\(^2\)]
Awọn alaye Idahun
We can use the formula for gravitational force between two masses: F = (G x m1 x m2)/r^2 where F = force of attraction G = gravitational constant m1 and m2 = masses of the bodies r = distance between the centers of the two bodies Plugging in the given values, we get: F = (6.67 x 10^-11 Nm^2/kg^2) x (3.0 kg) x (2.0 kg) / (0.50 m)^2 F = 1.6 x 10^-9 N Therefore, the force of attraction between the two bodies is 1.6 x 10^-9 N. Answer: 1.6 x 10^-9 N
Ibeere 15 Ìròyìn
Which of the following graphs gives the correct relationship between energy and mass when mass is converted to energy.
Awọn alaye Idahun
Ibeere 16 Ìròyìn
Which of the following thermometers is used to measure the temperature of the human body?
Awọn alaye Idahun
Ibeere 17 Ìròyìn
Which of the following devices is used for storing electric charges?
Awọn alaye Idahun
A capacitor is a device that is used for storing electric charges. It consists of two conductive plates separated by an insulating material called a dielectric. When a voltage is applied to the capacitor, electric charges are stored on the plates. The amount of charge that can be stored on a capacitor is proportional to the voltage applied and the capacitance of the capacitor, which is a measure of its ability to store electric charges. A transformer is a device that is used to change the voltage of an alternating current (AC) electrical supply. It works by using electromagnetic induction to transfer energy from one coil of wire to another. An ammeter is a device that is used to measure the current in an electrical circuit. It works by detecting the flow of electric charges through a conductor and measuring the resulting electric potential difference. A potentiometer is a device that is used to measure the potential difference (voltage) between two points in an electrical circuit. It works by comparing the voltage being measured to a reference voltage, and it can also be used to adjust the voltage in a circuit. Therefore, a capacitor is the device used for storing electric charges.
Ibeere 18 Ìròyìn
A freshly demagnetized bar magnet is placed in the East-West direction to ensure that
Awọn alaye Idahun
Placing a freshly demagnetized bar magnet in the East-West direction helps ensure that the molecular magnets within the magnet remain randomly arranged. This is because, in this position, the magnet is perpendicular to the Earth's magnetic field, which would otherwise affect the alignment of the molecular magnets. By keeping the molecular magnets in a random arrangement, the magnet can be effectively demagnetized and can be magnetized again in a desired direction.
Ibeere 19 Ìròyìn
A ray of light traveling from a rectangular glass block of refractive index 1.5 into air strikes the block at an angle of incidence of 30. Calculate its angle of refraction.
Awọn alaye Idahun
The angle of refraction of a ray of light traveling from one medium to another can be calculated using Snell's law. Snell's law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the indices of refraction of the two media. Mathematically, this can be expressed as: sin θincidence / sin θrefraction = n1 / n2 Where θincidence is the angle of incidence, θrefraction is the angle of refraction, n1 is the index of refraction of the first medium, and n2 is the index of refraction of the second medium. Given the angle of incidence of 30° and the indices of refraction of 1.5 for the rectangular glass block and 1.0 for air, we can calculate the angle of refraction as follows: sin θincidence / sin θrefraction = n1 / n2 sin 30° / sin θrefraction = 1.5 / 1.0 sin θrefraction = sin 30° / 1.5 θrefraction = sin-1(sin 30° / 1.5) = 19.47° Therefore, the angle of refraction of the ray of light traveling from the rectangular glass block into air is approximately 19.47°.
Ibeere 20 Ìròyìn
A rectangular piece of iron measuring 4 cm by 3 cm at 20\(^o\)C is heated until its temperature increases by 100 C. Calculate the new area of the metal. [Linear expansivity of iron is 1.2x 10\(^{-5}\) K\(^{-1}\)]
Awọn alaye Idahun
The change in the area of a rectangular piece of iron due to an increase in temperature can be calculated using the formula for linear expansion: ΔL = α * L * ΔT Where ΔL is the change in length, α is the linear expansivity, L is the original length, and ΔT is the change in temperature. The new length of the iron can be calculated by adding the change in length to the original length: L' = L + ΔL The new area of the iron can be calculated by using the new length and width: A' = L' * W First, the change in length of the iron can be calculated for both the length and the width: ΔL = α * L * ΔT = 1.2 x 10^-5 K^-1 * 4 cm * 100°C = 4.8 x 10^-3 cm L' = L + ΔL = 4 cm + 4.8 x 10^-3 cm = 4.0048 cm ΔL = α * L * ΔT = 1.2 x 10^-5 K^-1 * 3 cm * 100°C = 3.6 x 10^-3 cm W' = W + ΔL = 3 cm + 3.6 x 10^-3 cm = 3.0036 cm The new area of the iron can be calculated using the new length and width: A' = L' * W' = 4.0048 cm * 3.0036 cm = 12.0288 cm^2 Therefore, the new area of the metal after a temperature increase of 100°C is 12.0288 cm^2.
Ibeere 21 Ìròyìn
The diagram above illustrates a meter bridge circuit under balanced condition. Determine the value of x.
Awọn alaye Idahun
Ibeere 22 Ìròyìn
A transverse pulse of frequency 9 Hz traves 4.5m in 0.6 s. Calculate the wavelength of the pulse.
Awọn alaye Idahun
The formula for the speed of a wave is given by: v = λf where v is the speed of the wave, λ is the wavelength, and f is the frequency. We are given the frequency of the pulse as 9 Hz and the time it takes to travel a distance of 4.5 m as 0.6 s. We can use these values to calculate the speed of the pulse as follows: v = d/t = 4.5 m/0.6 s = 7.5 m/s Now, we can use the formula v = λf to calculate the wavelength of the pulse: λ = v/f = 7.5 m/s / 9 Hz = 0.83 m Therefore, the wavelength of the pulse is 0.83 m. Answer option (C) is correct.
Ibeere 23 Ìròyìn
When ultraviolet light is incident on certain metallic p articles are emitted. These particles are called
Ibeere 24 Ìròyìn
The vacuum in a thermoflask reduces heat loss resulting from
Awọn alaye Idahun
The vacuum in a thermoflask reduces heat loss resulting from conduction and convection by creating a space with no air molecules between the inner and outer layers of the flask, which minimizes heat transfer through these processes. Additionally, the reflective surfaces of the inner layer further minimize heat loss by reflecting any radiation back into the flask.
Ibeere 25 Ìròyìn
The induced current in a coil always flows in a direction so as to oppose the change that causes it. This statement is known as
Awọn alaye Idahun
Lenz's law states that the induced current in a coil always flows in a direction so as to oppose the change that causes it. For example, if there is a change in magnetic flux passing through a coil, it will induce an electromotive force (EMF) and a current will start flowing in the coil. This induced current will create a magnetic field that opposes the original change in magnetic flux. Lenz's law is a consequence of the law of conservation of energy and is a fundamental law in electromagnetism.
Ibeere 26 Ìròyìn
A device consumes 100 W of power when connected to a 120 V source. Calculate its resistance.
Awọn alaye Idahun
Ibeere 27 Ìròyìn
An instrument used to measure relative humidity is the?
Awọn alaye Idahun
An instrument used to measure relative humidity is the hygrometer. Hygrometers measure the amount of water vapor present in the air, which is an indicator of the air's relative humidity. Hygrometers can be mechanical or electronic, and they may measure relative humidity directly or calculate it from measurements of temperature and dew point.
Ibeere 29 Ìròyìn
Which of the following properties is not exhibited by sound waves?
Awọn alaye Idahun
The property that is not exhibited by sound waves is polarization. Polarization is a property of transverse waves, which are waves that vibrate perpendicular to the direction of their motion. Sound waves, on the other hand, are longitudinal waves, which means that they vibrate parallel to the direction of their motion. Since sound waves are not transverse, they cannot exhibit polarization. Diffraction, interference, and reflection are all properties of sound waves. Diffraction is the bending of sound waves around obstacles or through openings. Interference occurs when two or more sound waves interact with each other, either constructively or destructively. Reflection is the bouncing back of sound waves when they hit a surface. In summary, sound waves are longitudinal waves and cannot exhibit polarization, but they can exhibit other properties such as diffraction, interference, and reflection.
Ibeere 30 Ìròyìn
Which of the following graphs of a charge Q against potential difference V across the capacitor is correct?
Awọn alaye Idahun
Ibeere 31 Ìròyìn
The time rate of increase in velocity is called
Awọn alaye Idahun
The time rate of increase in velocity is called acceleration. Acceleration is a measure of how quickly an object changes its velocity, and it is calculated as the change in velocity per unit of time. Velocity is a vector quantity that describes an object's speed and direction of motion. If an object's velocity changes over time, either in magnitude (speed) or direction, it is said to be accelerating. The acceleration of an object is the rate at which its velocity changes, and it is a measure of the force acting on an object. Force is a vector quantity that describes the interaction between two objects that results in a change in motion. Force is proportional to acceleration, so a greater force will result in a greater acceleration. Momentum is a vector quantity that describes an object's mass and velocity. Momentum is conserved in an isolated system, meaning that the total momentum of the system remains constant, although the momentum of individual objects within the system may change. Speed is a scalar quantity that describes the magnitude of an object's velocity, without considering its direction. Speed is a measure of how quickly an object is moving, but it does not take into account changes in direction. Therefore, the time rate of increase in velocity is called acceleration.
Ibeere 32 Ìròyìn
A body of mass 2 kg is released from a point 100 m above the ground. Calculate its kinetic energy 80m from the point of release.
Awọn alaye Idahun
Ibeere 33 Ìròyìn
The diagram above represents an experimental set-up for verifying?
Ibeere 34 Ìròyìn
In an elastic collision, momentum is conserved as well as well as?
Awọn alaye Idahun
In an elastic collision, both momentum and kinetic energy are conserved. Momentum is defined as the product of an object's mass and velocity, and it is a measure of an object's motion. In an elastic collision, the total momentum before the collision is equal to the total momentum after the collision. This means that the momentum of the objects involved in the collision is conserved. Kinetic energy is defined as the energy an object possesses due to its motion. In an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision. This means that the kinetic energy of the objects involved in the collision is conserved. In contrast, potential energy is a measure of an object's potential to do work, and it is related to an object's position or configuration. In an elastic collision, potential energy is not conserved because the objects change position or configuration during the collision. Therefore, in an elastic collision, momentum and kinetic energy are conserved, while potential energy is not conserved.
Ibeere 35 Ìròyìn
A small amount of air is introduced into the vacuum above the mercury in a mercury barometer tube. The mercury level goes down because the air molecules
Awọn alaye Idahun
Ibeere 36 Ìròyìn
Which of the following characteristics of waves can a ripple tank be used to demonstrate?
I. Reflection
II. Refraction
III. Diffraction
Awọn alaye Idahun
A ripple tank is a scientific apparatus that can be used to demonstrate the behavior of waves. It produces waves on the surface of water that can be observed and studied. I. Reflection: When waves encounter a boundary or obstacle, they can bounce back or reflect. A ripple tank can be used to demonstrate reflection by placing a barrier in the path of the waves and observing how they bounce back. II. Refraction: Waves can also change direction or bend when they pass through a medium with a different density or refractive index. A ripple tank can demonstrate refraction by placing a block in the path of the waves and observing how they change direction as they pass through it. III. Diffraction: When waves encounter an obstacle with a small opening or gap, they can bend and spread out, creating a diffraction pattern. A ripple tank can demonstrate diffraction by creating waves with a single source and observing how they spread out as they pass through a gap or opening. Therefore, the correct answer is "I, II and III".
Ibeere 37 Ìròyìn
Which of the following statements about a neutral atom is correct? The
Awọn alaye Idahun
A neutral atom is an atom that has an equal number of protons and electrons. The protons are located in the nucleus of the atom, along with the neutrons, and the electrons occupy the space surrounding the nucleus. The number of protons in the nucleus of an atom determines the chemical element to which it belongs. A neutral atom has no overall charge, meaning that the positive charge of the protons is balanced by the negative charge of the electrons. Hence, the correct statement about a neutral atom is that the number of protons is equal to that of electrons.
Ibeere 39 Ìròyìn
The mass of a load is doubled while the force acting on it is halved. The resulting acceleration of the load is
Awọn alaye Idahun
Ibeere 40 Ìròyìn
Which of the following waves is not mechanical?
Awọn alaye Idahun
The main idea of this question is to identify a type of wave that is not mechanical. Mechanical waves require a medium to travel through, such as a solid, liquid or gas. Sound waves and water waves are examples of mechanical waves. On the other hand, radio waves are a type of electromagnetic wave and do not require a medium to travel through. Therefore, the answer to the question is "Radio waves."
Ibeere 41 Ìròyìn
Which of the following statements about a moving object is correct?
Awọn alaye Idahun
The correct statement about a moving object is "At a steady velocity, the resultant force acting on it must be equal to zero." This means that when an object is moving at a constant speed in a straight line (i.e., at a steady velocity), the net force acting on it is zero. This does not mean that there are no forces acting on the object, but rather that the forces are balanced such that they cancel each other out. If the object were to accelerate or decelerate, there would be a net force acting on it. Similarly, air resistance can be a force acting on the object but it does not need to be zero for the object to move at a steady velocity, as long as it is balanced by other forces.
Ibeere 42 Ìròyìn
Which property of a wave remains constant when the wave travels from one medium into another?
Awọn alaye Idahun
Ibeere 43 Ìròyìn

In the diagram above, the time taken to trace a wave between P and Q is
Awọn alaye Idahun
Ibeere 45 Ìròyìn
An electron of mass 9.1 x 10\(^{-31}\) kg moves with a speed of 2.0 x 10\(^6\) ms\(^{-1}\) round the nucleus of an atom in a Circular path of radius
6.1 x 10\(^{11}\) m. Calculate the centripetal force acting on the electron.
Awọn alaye Idahun
The centripetal force acting on an electron moving in a circular path around the nucleus of an atom is given by the equation: F = (mv\(^2\))/r Where F is the centripetal force, m is the mass of the electron, v is the velocity of the electron, and r is the radius of the circular path. Substituting the given values into the equation, we have: F = (9.1 x 10\(^{-31}\) kg) x (2.0 x 10\(^6\) ms\(^{-1}\))\(^2\) / (6.1 x 10\(^{11}\) m) F = 6.0 x 10\(^{-8}\) N Therefore, the correct answer is: 6.0 x 10\(^{-8}\) N.
Ibeere 46 Ìròyìn
The anomalous expansion of water occurs in the range
Awọn alaye Idahun
The anomalous expansion of water refers to a phenomenon in which water expands instead of contracting as it cools below a certain temperature. This is a unique property of water, as most substances contract when they cool. The temperature range in which the anomalous expansion of water occurs is from 4°C to 0°C. As water cools below 4°C, it starts to contract, but as it approaches 0°C, it expands again. This means that at 0°C, water is actually less dense than it is at 4°C. Therefore, the answer is: 0°C to 4°C. This is the temperature range in which the anomalous expansion of water occurs.
Ibeere 47 Ìròyìn
An electron of mass 9.1 x 10\(^{-31}\) kg moves with a speed of 2.0 x 10\(^6\) ms\(^{-1}\) round the nucleus of an atom in a Circular path of radius 6.1 x 10(^{11}\) m. Determine the angular speed of the electron.
Awọn alaye Idahun
The angular speed of the electron can be determined using the formula: ω = v / r where ω is the angular speed, v is the velocity of the electron, and r is the radius of the circular path. Substituting the given values, we get: ω = (2.0 x 10^6 m/s) / (6.1 x 10^11 m) ω = 3.28 x 10^(-5) rad/s Therefore, the angular speed of the electron is 3.28 x 10^(-5) rad/s. Hence, the correct option is: 3.28 x 10^16 rad s^(-1)
Ibeere 48 Ìròyìn
The diagram above illustrates an object moving in a circular path at a constant speed. Which of the arrows indicates the direction of linear velocity?
Awọn alaye Idahun
Ibeere 49 Ìròyìn
Which of the following cases cannot produce total internal reflection? A light ray travelling from
Awọn alaye Idahun
Ibeere 50 Ìròyìn
(a) State the principle of operation of fibre optics.
(b) State two applications of fibre optics in medicine.
(a) The principle of operation of fiber optics is based on the concept of total internal reflection. Light is carried through a thin, flexible fiber made of glass or plastic. The inner core of the fiber has a higher refractive index than the outer cladding, which has a lower refractive index. When light enters the fiber, it is reflected multiple times off the core-cladding interface, and travels along the fiber due to total internal reflection. This allows the light to be transmitted over long distances without significant loss of energy or degradation of the signal.
(b) Fiber optics has many applications in medicine, including:
-
Medical imaging: Fiber optic cables can be used to transmit images from inside the body to an external device. For example, endoscopes use fiber optics to provide high-quality images of the digestive or respiratory systems.
-
Illumination: Fiber optics can also be used to provide light in medical procedures, such as laparoscopic surgery. The light source is positioned outside the body, and the light is transmitted to the surgical site via a fiber optic cable. This allows for bright, even illumination without exposing the patient to direct light.
Awọn alaye Idahun
(a) The principle of operation of fiber optics is based on the concept of total internal reflection. Light is carried through a thin, flexible fiber made of glass or plastic. The inner core of the fiber has a higher refractive index than the outer cladding, which has a lower refractive index. When light enters the fiber, it is reflected multiple times off the core-cladding interface, and travels along the fiber due to total internal reflection. This allows the light to be transmitted over long distances without significant loss of energy or degradation of the signal.
(b) Fiber optics has many applications in medicine, including:
-
Medical imaging: Fiber optic cables can be used to transmit images from inside the body to an external device. For example, endoscopes use fiber optics to provide high-quality images of the digestive or respiratory systems.
-
Illumination: Fiber optics can also be used to provide light in medical procedures, such as laparoscopic surgery. The light source is positioned outside the body, and the light is transmitted to the surgical site via a fiber optic cable. This allows for bright, even illumination without exposing the patient to direct light.
Ibeere 51 Ìròyìn
A stone of mass 20g is released from a catapult whose rubber is stretched through 5cm. If the force constant of the rubber is 200Nm\(^{-1}\), calculate the speed with which the stone leaves the catapult.
To solve this problem, we need to use the principle of conservation of energy, which states that the initial energy of the system is equal to the final energy of the system. Initially, the rubber band has potential energy stored in it due to its stretching, which is then transferred to the stone when it is released. This potential energy is converted into kinetic energy as the stone is propelled forward.
The potential energy stored in the rubber band can be calculated using the formula:
PE = 0.5 * k * x^2
where PE is the potential energy, k is the force constant of the rubber band, and x is the distance the rubber band is stretched.
In this case, PE = 0.5 * 200 N/m * (0.05 m)^2 = 0.5 J
Since the potential energy is converted to kinetic energy when the stone is released, we can equate the two and solve for the velocity of the stone:
PE = KE
0.5 * m * v^2 = 0.5 J
where m is the mass of the stone and v is its velocity.
Rearranging this equation, we get:
v = sqrt(2 * PE / m)
Substituting the values we have, we get:
v = sqrt(2 * 0.5 J / 0.02 kg) = 5 m/s
Therefore, the speed with which the stone leaves the catapult is 5 m/s.
Awọn alaye Idahun
To solve this problem, we need to use the principle of conservation of energy, which states that the initial energy of the system is equal to the final energy of the system. Initially, the rubber band has potential energy stored in it due to its stretching, which is then transferred to the stone when it is released. This potential energy is converted into kinetic energy as the stone is propelled forward.
The potential energy stored in the rubber band can be calculated using the formula:
PE = 0.5 * k * x^2
where PE is the potential energy, k is the force constant of the rubber band, and x is the distance the rubber band is stretched.
In this case, PE = 0.5 * 200 N/m * (0.05 m)^2 = 0.5 J
Since the potential energy is converted to kinetic energy when the stone is released, we can equate the two and solve for the velocity of the stone:
PE = KE
0.5 * m * v^2 = 0.5 J
where m is the mass of the stone and v is its velocity.
Rearranging this equation, we get:
v = sqrt(2 * PE / m)
Substituting the values we have, we get:
v = sqrt(2 * 0.5 J / 0.02 kg) = 5 m/s
Therefore, the speed with which the stone leaves the catapult is 5 m/s.
Ibeere 52 Ìròyìn
(a) Define diffusion
(b) State two factors that affect the rate of diffusion
(a) Diffusion is the movement of particles (atoms, molecules, or ions) from an area of high concentration to an area of low concentration. This process occurs naturally and spontaneously and is driven by the random motion of particles.
(b) Two factors that affect the rate of diffusion are:
(i) Temperature: As the temperature increases, the kinetic energy of the particles also increases, which leads to faster movement and increased collision frequency. This results in a higher rate of diffusion.
(ii) Concentration gradient: The greater the difference in concentration between two areas, the faster the rate of diffusion. This is because the concentration gradient provides a driving force for the movement of particles from high concentration to low concentration. Therefore, a steeper concentration gradient will result in a higher rate of diffusion.
Awọn alaye Idahun
(a) Diffusion is the movement of particles (atoms, molecules, or ions) from an area of high concentration to an area of low concentration. This process occurs naturally and spontaneously and is driven by the random motion of particles.
(b) Two factors that affect the rate of diffusion are:
(i) Temperature: As the temperature increases, the kinetic energy of the particles also increases, which leads to faster movement and increased collision frequency. This results in a higher rate of diffusion.
(ii) Concentration gradient: The greater the difference in concentration between two areas, the faster the rate of diffusion. This is because the concentration gradient provides a driving force for the movement of particles from high concentration to low concentration. Therefore, a steeper concentration gradient will result in a higher rate of diffusion.
Ibeere 53 Ìròyìn
State three observable phenomena in which waves behave like a particle.
The phenomena in which waves behave like a particle are collectively known as wave-particle duality. Here are three observable phenomena that demonstrate this concept:
-
Photoelectric effect: When light is shone on a metal surface, electrons are emitted from the surface. This can be explained by the idea that light behaves as a stream of particles called photons. These photons collide with the electrons in the metal, causing them to be ejected from the surface.
-
Compton scattering: When X-rays are scattered off a material, the wavelength of the scattered X-rays is longer than the incident X-rays. This can be explained by the idea that X-rays behave like particles, and when they collide with electrons in the material, they transfer some of their energy to the electrons, causing the X-rays to lose energy and their wavelength to increase.
-
Electron diffraction: When a beam of electrons is passed through a crystal, it produces a diffraction pattern that is similar to the pattern produced by a beam of light passing through a diffraction grating. This can be explained by the idea that electrons behave like waves, and their wavelength is related to their momentum. The crystal acts as a diffraction grating, causing the electrons to diffract and interfere with each other, producing the characteristic pattern.
Awọn alaye Idahun
The phenomena in which waves behave like a particle are collectively known as wave-particle duality. Here are three observable phenomena that demonstrate this concept:
-
Photoelectric effect: When light is shone on a metal surface, electrons are emitted from the surface. This can be explained by the idea that light behaves as a stream of particles called photons. These photons collide with the electrons in the metal, causing them to be ejected from the surface.
-
Compton scattering: When X-rays are scattered off a material, the wavelength of the scattered X-rays is longer than the incident X-rays. This can be explained by the idea that X-rays behave like particles, and when they collide with electrons in the material, they transfer some of their energy to the electrons, causing the X-rays to lose energy and their wavelength to increase.
-
Electron diffraction: When a beam of electrons is passed through a crystal, it produces a diffraction pattern that is similar to the pattern produced by a beam of light passing through a diffraction grating. This can be explained by the idea that electrons behave like waves, and their wavelength is related to their momentum. The crystal acts as a diffraction grating, causing the electrons to diffract and interfere with each other, producing the characteristic pattern.
Ibeere 54 Ìròyìn
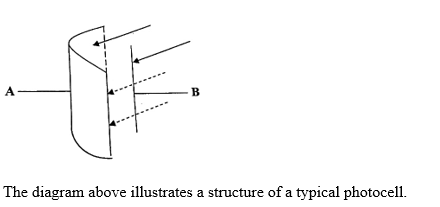
The diagram above illustrates a structure of a typical photocell.
(i) Identify each of the parts labelled A and B.
(ii) State one function each of A and B
(iii) Einstein’s photoelectric equation can be written as E = hf – Wo. State what each of the terms E, hf and Wo represent.
(b) A photon is incident on a metal whose work function is 1.32 eV. An electron is emitted from the surface with a maximum kinetic energy of 1.97 eV. Calculate the frequency of the photon. [1 eV = 1.6 x 10-19 J]
(c)(i) Define half-life of a radioactive element.
(ii) Sketch a graph of the relation N = Noe-λt and indicate the half-life.
(a)
(i) A - Metal surface, B - Collector electrode
(ii) A - To emit electrons when photons hit its surface, B - To collect the emitted electrons and create a current.
(iii) E represents the energy of the photon, hf represents the energy of the photon before it hits the metal surface, and Wo represents the work function or the minimum energy required to remove an electron from the metal surface.
(b)
Using Einstein's photoelectric equation, we can write:
hf = E + Wo
where hf is the energy of the photon, E is the kinetic energy of the emitted electron, and Wo is the work function.
We know that E = 1.97 eV and Wo = 1.32 eV. Converting to joules, we have:
E = 1.97 x 1.6 x 10^-19 J = 3.15 x 10^-19 J
Wo = 1.32 x 1.6 x 10^-19 J = 2.11 x 10^-19 J
Substituting these values into the equation:
hf = E + Wo = 3.15 x 10^-19 J + 2.11 x 10^-19 J = 5.26 x 10^-19 J
Finally, using the formula for the energy of a photon:
E = hf = hc/λ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the photon. Solving for λ, we get:
λ = hc/E = (6.626 x 10^-34 J s x 3.0 x 10^8 m/s) / 5.26 x 10^-19 J = 3.77 x 10^-7 m
So, the frequency of the photon is:
f = c/λ = 3.0 x 10^8 m/s / 3.77 x 10^-7 m = 7.96 x 10^14 Hz
(c)
(i) The half-life of a radioactive element is the time taken for half of the radioactive nuclei to decay.
(ii) The graph of the relation N = Noe^-λt is an exponential decay curve. The half-life can be found by setting N = 0.5No and solving for t. This gives:
0.5No = Noe^-λt
Taking the natural logarithm of both sides, we get:
ln(0.5) = -λt1/2
where t1/2 is the half-life. Rearranging this equation, we get:
t1/2 = ln(2) / λ
The half-life is the time taken for the number of radioactive nuclei to reduce to half its initial value, as shown in the graph.
Awọn alaye Idahun
(a)
(i) A - Metal surface, B - Collector electrode
(ii) A - To emit electrons when photons hit its surface, B - To collect the emitted electrons and create a current.
(iii) E represents the energy of the photon, hf represents the energy of the photon before it hits the metal surface, and Wo represents the work function or the minimum energy required to remove an electron from the metal surface.
(b)
Using Einstein's photoelectric equation, we can write:
hf = E + Wo
where hf is the energy of the photon, E is the kinetic energy of the emitted electron, and Wo is the work function.
We know that E = 1.97 eV and Wo = 1.32 eV. Converting to joules, we have:
E = 1.97 x 1.6 x 10^-19 J = 3.15 x 10^-19 J
Wo = 1.32 x 1.6 x 10^-19 J = 2.11 x 10^-19 J
Substituting these values into the equation:
hf = E + Wo = 3.15 x 10^-19 J + 2.11 x 10^-19 J = 5.26 x 10^-19 J
Finally, using the formula for the energy of a photon:
E = hf = hc/λ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the photon. Solving for λ, we get:
λ = hc/E = (6.626 x 10^-34 J s x 3.0 x 10^8 m/s) / 5.26 x 10^-19 J = 3.77 x 10^-7 m
So, the frequency of the photon is:
f = c/λ = 3.0 x 10^8 m/s / 3.77 x 10^-7 m = 7.96 x 10^14 Hz
(c)
(i) The half-life of a radioactive element is the time taken for half of the radioactive nuclei to decay.
(ii) The graph of the relation N = Noe^-λt is an exponential decay curve. The half-life can be found by setting N = 0.5No and solving for t. This gives:
0.5No = Noe^-λt
Taking the natural logarithm of both sides, we get:
ln(0.5) = -λt1/2
where t1/2 is the half-life. Rearranging this equation, we get:
t1/2 = ln(2) / λ
The half-life is the time taken for the number of radioactive nuclei to reduce to half its initial value, as shown in the graph.
Ibeere 55 Ìròyìn
(a) (i) Define force and state its S.I unit.
(ii) List the two types of solid friction.
(b) A car travelling at a constant speed of 30 ms-1 for 20 s was suddenly decelerated when the driver sighted a pot-hole. It took the driver 6 s to get to the pot-hole with a reduced speed of 18 ms-1. He maintained the steady speed for another 10 s to cross the pot-hole. The brakes were then applied and the car came to rest 5 s later.
(i) Draw the velocity-time graph for the journey.
(ii) Calculate the deceleration during the last 5 s of the journey.
(iii) Calculate the total distance covered.
(a)
(i) Force is a push or pull acting on an object that causes it to accelerate or deform. The SI unit of force is newton (N).
(ii) The two types of solid friction are static friction and kinetic friction.
(b)
(i)
The velocity-time graph for the journey is shown above. The horizontal axis represents time in seconds, and the vertical axis represents velocity in meters per second (m/s). The graph shows that the car was travelling at a constant velocity of 30 m/s for 20 seconds, then decelerated to a velocity of 18 m/s over a period of 6 seconds, maintained that velocity for 10 seconds, and finally came to rest over a period of 5 seconds.
(ii)
To calculate the deceleration during the last 5 seconds of the journey, we can use the formula:
a = (vf - vi) / t
where a is the acceleration, vf is the final velocity, vi is the initial velocity, and t is the time interval. In this case, the final velocity is 0 m/s, the initial velocity is 18 m/s, and the time interval is 5 seconds. Therefore:
a = (0 - 18) / 5 = -3.6 m/s2
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity, which is consistent with deceleration.
(iii)
To calculate the total distance covered, we need to break the journey down into three parts:
- The distance covered while travelling at a constant velocity of 30 m/s for 20 seconds.
- The distance covered while decelerating from 30 m/s to 18 m/s over a period of 6 seconds, and then maintaining a constant velocity of 18 m/s for 10 seconds.
- The distance covered while coming to rest over a period of 5 seconds.
For part 1, the distance covered is:
distance = velocity x time distance = 30 m/s x 20 s = 600 m
For part 2, we need to calculate the average velocity over the 16-second period (6 seconds of deceleration + 10 seconds of constant velocity). The average velocity is:
average velocity = (initial velocity + final velocity) / 2 average velocity = (30 m/s + 18 m/s) / 2 = 24 m/s
The distance covered during this 16-second period is:
distance = velocity x time distance = 24 m/s x 16 s = 384 m
For part 3, the distance covered is:
distance = (final velocity / 2) x time distance = (0 m/s / 2)
Awọn alaye Idahun
(a)
(i) Force is a push or pull acting on an object that causes it to accelerate or deform. The SI unit of force is newton (N).
(ii) The two types of solid friction are static friction and kinetic friction.
(b)
(i)
The velocity-time graph for the journey is shown above. The horizontal axis represents time in seconds, and the vertical axis represents velocity in meters per second (m/s). The graph shows that the car was travelling at a constant velocity of 30 m/s for 20 seconds, then decelerated to a velocity of 18 m/s over a period of 6 seconds, maintained that velocity for 10 seconds, and finally came to rest over a period of 5 seconds.
(ii)
To calculate the deceleration during the last 5 seconds of the journey, we can use the formula:
a = (vf - vi) / t
where a is the acceleration, vf is the final velocity, vi is the initial velocity, and t is the time interval. In this case, the final velocity is 0 m/s, the initial velocity is 18 m/s, and the time interval is 5 seconds. Therefore:
a = (0 - 18) / 5 = -3.6 m/s2
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity, which is consistent with deceleration.
(iii)
To calculate the total distance covered, we need to break the journey down into three parts:
- The distance covered while travelling at a constant velocity of 30 m/s for 20 seconds.
- The distance covered while decelerating from 30 m/s to 18 m/s over a period of 6 seconds, and then maintaining a constant velocity of 18 m/s for 10 seconds.
- The distance covered while coming to rest over a period of 5 seconds.
For part 1, the distance covered is:
distance = velocity x time distance = 30 m/s x 20 s = 600 m
For part 2, we need to calculate the average velocity over the 16-second period (6 seconds of deceleration + 10 seconds of constant velocity). The average velocity is:
average velocity = (initial velocity + final velocity) / 2 average velocity = (30 m/s + 18 m/s) / 2 = 24 m/s
The distance covered during this 16-second period is:
distance = velocity x time distance = 24 m/s x 16 s = 384 m
For part 3, the distance covered is:
distance = (final velocity / 2) x time distance = (0 m/s / 2)
Ibeere 56 Ìròyìn
List three magnetic elements that determine the earth’s magnetic field at a point.
The Earth's magnetic field is generated by the motion of molten iron in its core. The magnetic field at a given point on the Earth's surface is determined by the orientation and strength of this magnetic field.
Three magnetic elements that determine the Earth's magnetic field at a point are:
1. Magnetic declination: This is the angle between true north and magnetic north. It is determined by the position of the observer relative to the Earth's magnetic field.
2. Magnetic inclination: This is the angle between the Earth's magnetic field lines and the horizontal plane. It is determined by the latitude of the observer.
3. Magnetic intensity: This is the strength of the Earth's magnetic field at a given point. It is determined by the position of the observer relative to the Earth's magnetic field and the strength of the field generated by the Earth's core.
Together, these three magnetic elements give us a complete picture of the Earth's magnetic field at a given point. They are important for navigation and other applications that rely on the Earth's magnetic field.
Awọn alaye Idahun
The Earth's magnetic field is generated by the motion of molten iron in its core. The magnetic field at a given point on the Earth's surface is determined by the orientation and strength of this magnetic field.
Three magnetic elements that determine the Earth's magnetic field at a point are:
1. Magnetic declination: This is the angle between true north and magnetic north. It is determined by the position of the observer relative to the Earth's magnetic field.
2. Magnetic inclination: This is the angle between the Earth's magnetic field lines and the horizontal plane. It is determined by the latitude of the observer.
3. Magnetic intensity: This is the strength of the Earth's magnetic field at a given point. It is determined by the position of the observer relative to the Earth's magnetic field and the strength of the field generated by the Earth's core.
Together, these three magnetic elements give us a complete picture of the Earth's magnetic field at a given point. They are important for navigation and other applications that rely on the Earth's magnetic field.
Ibeere 57 Ìròyìn
(a) (i) Explain latent heat.
(ii) State two factors that affect the rate of evaporation of a liquid
(b) Explain each of the following observations:
(i) On a dry day, water in a clay pot is cooler than water in a closed plastic container;
(ii) Food gets cooked faster in a pressure cooker than in an ordinary cooking pot.
(c) State two effects of heat on a substance.
(d) A 40 V electric heater is used to supply a current of 12 A for 1400 s to a body of mass 1.5 kg at the melting point of the body. The body melts and its temperature rises through 60\(^o\)C in an extra 72 s. Determine the:
(i) latent heat of fusion of the body;
(ii)specific heat capacity of the body.
(a)
(i) Latent heat is the amount of heat energy required to change the state of a substance without changing its temperature. This means that the energy is either absorbed or released during a change in state, such as during melting, evaporation, or condensation.
(ii) The rate of evaporation of a liquid is affected by two main factors: temperature and surface area. As temperature increases, the rate of evaporation increases because more energy is available to break the bonds between liquid molecules. A larger surface area also increases the rate of evaporation because more liquid molecules are exposed to the air, allowing for more frequent collisions and evaporation.
(b)
(i) Water in a clay pot is cooler than water in a closed plastic container on a dry day because of evaporation. The porous surface of the clay pot allows for water to seep through and evaporate, which removes heat from the remaining water and causes it to cool. In contrast, a closed plastic container does not allow for evaporation, so the water remains at the same temperature.
(ii) Food gets cooked faster in a pressure cooker than in an ordinary cooking pot because of increased pressure and temperature. When the pressure is increased in a sealed container, the boiling point of water increases, which means that food can be cooked at a higher temperature. This higher temperature allows for faster cooking because it breaks down the food faster and more thoroughly.
(c)
Two effects of heat on a substance are expansion and change in state. When a substance is heated, its particles gain more energy and move faster, causing them to spread out and take up more space, leading to expansion. Also, when heat is added or removed from a substance, it can change its state from solid to liquid or from liquid to gas, or vice versa.
(d)
(i) The latent heat of fusion of the body can be calculated using the formula Q = mL, where Q is the heat energy required, m is the mass of the substance, and L is the latent heat of fusion. First, we need to calculate the heat energy required to melt the body: Q = VIt = (40V)(12A)(1400s) = 6.72 x 10^6 J. Next, we need to calculate the heat energy required to raise the temperature of the body by 60°C: Q = mcΔT = (1.5kg)(4200 J/kg°C)(60°C) = 3.78 x 10^5 J. Therefore, the total heat energy required is 7.08 x 10^6 J. Since the heat energy required for melting is equal to the product of the mass and latent heat of fusion, we can calculate the latent heat of fusion as L = Q/m = (6.72 x 10^6 J)/(1.5 kg) = 4.48 x 10^6 J/kg.
(ii) The specific heat capacity of the body can be calculated using the same formula as before, Q = mcΔT, where Q is the heat energy required, m is the mass of the substance, c is the specific heat capacity, and ΔT is the change in temperature. We know that the heat energy required to raise the temperature of the body by 60°C is 3.78 x 10^5 J, and we know that the mass of the body is
Awọn alaye Idahun
(a)
(i) Latent heat is the amount of heat energy required to change the state of a substance without changing its temperature. This means that the energy is either absorbed or released during a change in state, such as during melting, evaporation, or condensation.
(ii) The rate of evaporation of a liquid is affected by two main factors: temperature and surface area. As temperature increases, the rate of evaporation increases because more energy is available to break the bonds between liquid molecules. A larger surface area also increases the rate of evaporation because more liquid molecules are exposed to the air, allowing for more frequent collisions and evaporation.
(b)
(i) Water in a clay pot is cooler than water in a closed plastic container on a dry day because of evaporation. The porous surface of the clay pot allows for water to seep through and evaporate, which removes heat from the remaining water and causes it to cool. In contrast, a closed plastic container does not allow for evaporation, so the water remains at the same temperature.
(ii) Food gets cooked faster in a pressure cooker than in an ordinary cooking pot because of increased pressure and temperature. When the pressure is increased in a sealed container, the boiling point of water increases, which means that food can be cooked at a higher temperature. This higher temperature allows for faster cooking because it breaks down the food faster and more thoroughly.
(c)
Two effects of heat on a substance are expansion and change in state. When a substance is heated, its particles gain more energy and move faster, causing them to spread out and take up more space, leading to expansion. Also, when heat is added or removed from a substance, it can change its state from solid to liquid or from liquid to gas, or vice versa.
(d)
(i) The latent heat of fusion of the body can be calculated using the formula Q = mL, where Q is the heat energy required, m is the mass of the substance, and L is the latent heat of fusion. First, we need to calculate the heat energy required to melt the body: Q = VIt = (40V)(12A)(1400s) = 6.72 x 10^6 J. Next, we need to calculate the heat energy required to raise the temperature of the body by 60°C: Q = mcΔT = (1.5kg)(4200 J/kg°C)(60°C) = 3.78 x 10^5 J. Therefore, the total heat energy required is 7.08 x 10^6 J. Since the heat energy required for melting is equal to the product of the mass and latent heat of fusion, we can calculate the latent heat of fusion as L = Q/m = (6.72 x 10^6 J)/(1.5 kg) = 4.48 x 10^6 J/kg.
(ii) The specific heat capacity of the body can be calculated using the same formula as before, Q = mcΔT, where Q is the heat energy required, m is the mass of the substance, c is the specific heat capacity, and ΔT is the change in temperature. We know that the heat energy required to raise the temperature of the body by 60°C is 3.78 x 10^5 J, and we know that the mass of the body is
Ibeere 58 Ìròyìn
TEST OF PRACTICAL KNOWLEDGE QUESTION
You are provided with a converging lens and holder, a screen, a ray box containing an illuminated object pin, and a meter rule.
i. Place the lens in its holder such that it is facing a distant object seen through a well-lit laboratory window. Move the screen to and fro until a sharp image of the distant object is formed on it. Measure the distance, f\(_{0}\), between the screen and the lens.
ii. Clamp the meter rule securely to the table. Place the illuminated object pin at the end R of the meter rule.
iii. Place the lens at a position P such that X = RP = 20cm.
iv. Move the screen to a position Q to receive a sharp image of the object. Measure the distance Y = PQ.
v. Evaluate Z = (X+Y)
vi. Repeat the procedure for five other values of x = 25cm. 3Ocm, 35cm, 40cm and 45cm. In each case, record X,Y and evaluate Z.
vii. Tabulate the results.
viii. Plot a graph with Z on the vertical axis and X on the horizontal axis. Draw a smooth curve through the points.
ix. Determine from your graph the minimum value of Z=Z\(_{0}\) and its corresponding distance
x. Evaluate W = ½ (\(\frac{Z_0}{4} + \frac{X_0}{2}\))
xi. State two precautions taken to ensure accurate results.
(b) i. Draw a ray diagram to show how a Convex lens forms an image of magnification less than one.
ii. Name two pairs of features in the human eye and a lens camera that performs similar functions.
F = 13.0cm
Table of value
| S/N | Xcm | Ycm | Z(x+y)cm |
| 1 2 3 4 5 6 |
20 25 30 35 40 45 |
60 38 30 26 24 21 |
80 63 60 61 64 61 |
Let 1cm represent5 units on the vertical axis and 1cm represent 5 units on the horizontal axis.
Minimum value of Z=Z0
from the graph = 60cm
Corresponding distance of X0
= 30cm
Evaluate W
= ½ (Z04+X02 )
= ½(6040+302
= ½(60+604 = ½1204
= ½(30) = 15
Precautions
- Coaxial arrangement of optional instruments/ray box, len and screen on a straight line.
- Avoided parallax error in reading metre rule.
- Lens kept uptight
- Repeated reading shown on table
- Surface of lens cleaned
- Noted/corrected/avoided zero error on metre rule.
(b)
i.
ii. Features performing the same function
| Human eye | Lens camera |
| Retina | Film/screen |
| Eye lens | Camera lens |
| Iris | Diaphragm |
| Pupil | Aperture |
Awọn alaye Idahun
F = 13.0cm
Table of value
| S/N | Xcm | Ycm | Z(x+y)cm |
| 1 2 3 4 5 6 |
20 25 30 35 40 45 |
60 38 30 26 24 21 |
80 63 60 61 64 61 |
Let 1cm represent5 units on the vertical axis and 1cm represent 5 units on the horizontal axis.
Minimum value of Z=Z0
from the graph = 60cm
Corresponding distance of X0
= 30cm
Evaluate W
= ½ (Z04+X02 )
= ½(6040+302
= ½(60+604 = ½1204
= ½(30) = 15
Precautions
- Coaxial arrangement of optional instruments/ray box, len and screen on a straight line.
- Avoided parallax error in reading metre rule.
- Lens kept uptight
- Repeated reading shown on table
- Surface of lens cleaned
- Noted/corrected/avoided zero error on metre rule.
(b)
i.
ii. Features performing the same function
| Human eye | Lens camera |
| Retina | Film/screen |
| Eye lens | Camera lens |
| Iris | Diaphragm |
| Pupil | Aperture |
Ibeere 59 Ìròyìn
TEST OF PRACTICAL KNOWLEDGE QUESTION
You are provided with a battery of e.m.f. E, a key K, a voltmeter, a standard resistor R\(_{0}\) = 2\(\Omega\), a resistance box R, and some connecting wires.
i. Measure and record the e.m.f. E of the battery.
i. Set up a circuit as shown in the diagram above with the key open.
iii. Set the resistance on the resistance box to R 22.
iv. Close the key, read and record the potential difference V on the voltmeter.
v. Evaluate V\(^{-1}\)
vi. Repeat the procedures for five other values of R = 5\(\Omega\) 10\(\Omega\),12\(\Omega\),15\(\Omega\) and 20\(\Omega\). In each case, record V and evaluate V\(^{-1}\)
vii. Tabulate the results.
viii. Plot a graph with R on the vertical axis and V\(^{-1}\) l on the horizontal axis, starting both axes from the origin (0,0).
ix. Determine the slope, s, of the graph and the intercept c on the vertical axis.
x. Calculate \(\propto\) and \(\beta\) from the equations s = R\(_{0}\) \(\propto\) and c= - (R\(_{0}\)+B).
xi. State two precautions taken to obtain accurate results.
R0 = 2Ω , emf of the battery = 2.0V
Table of value
| S/N | RΩ | V | V |
| 1 2 3 4 5 6 |
2 5 10 12 15 20 |
4.70 2.40 1.75 1.40 1.10 0.76 |
0.214 0.417 0.571 0.714 0.909 1.320 |
Slope = △R△V−1 = 30.00−0.001.50−0.15
= 30.001.35 = 22
Intercept on the horizontal axis = 0.15
Calculation of ∝
∝ = SR0=222 = 11
Calculation of β
β
= -(R0
+ C) = - (2 + 0.15) = -(2.15) = -2.15
Precuations
- Key opened in between reading/key opened when readings were not taken.
- Tight connections ensured
- Avoided parallax error when taking reading on voltmetre
- Repeated readings shown on table
- Noted/corrected zero error on voltmetre
- Clean terminals ensured.
(b)
i. RAB = 4×54+5=209
PAB =VAB2RAB
= 42×920 = 7.2 W
ii. I = pv =3.6×103240
= 15A
The breaker will not open since the current drawn (15A) is less than (20A).
Awọn alaye Idahun
R0 = 2Ω , emf of the battery = 2.0V
Table of value
| S/N | RΩ | V | V |
| 1 2 3 4 5 6 |
2 5 10 12 15 20 |
4.70 2.40 1.75 1.40 1.10 0.76 |
0.214 0.417 0.571 0.714 0.909 1.320 |
Slope = △R△V−1 = 30.00−0.001.50−0.15
= 30.001.35 = 22
Intercept on the horizontal axis = 0.15
Calculation of ∝
∝ = SR0=222 = 11
Calculation of β
β
= -(R0
+ C) = - (2 + 0.15) = -(2.15) = -2.15
Precuations
- Key opened in between reading/key opened when readings were not taken.
- Tight connections ensured
- Avoided parallax error when taking reading on voltmetre
- Repeated readings shown on table
- Noted/corrected zero error on voltmetre
- Clean terminals ensured.
(b)
i. RAB = 4×54+5=209
PAB =VAB2RAB
= 42×920 = 7.2 W
ii. I = pv =3.6×103240
= 15A
The breaker will not open since the current drawn (15A) is less than (20A).
Ibeere 60 Ìròyìn
(a) (i) Define atomic spectra.
(ii) Differentiate between emission spectra and absorption spectra.
(b)
The diagram above illustrates an electron transition from energy level n = 3 to n = 1. Calculate the:
(i) energy of the photon
(ii) frequency of the photon
(ii) wavelength of the photon [h = 6.6 x 10\(^{-34}\)J s, c = 3.0 x 10\(^8\) ms\(^{-1}\); 1 ev = 1.6 x 10\(^{-19}\) J]
c)(i)Differentiate between soft x-rays and hard x-rays
(ii) Draw the circuit symbol for a p-n junction diode.
(iiii) Give the reason for doping a semiconductor material
a)
(i) Atomic spectra refers to the range of electromagnetic radiation emitted or absorbed by atoms. It is a characteristic of the arrangement of electrons in atoms and the energy changes that occur within them.
(ii) Emission spectra refer to the range of electromagnetic radiation emitted by an atom when it transitions from a higher energy level to a lower energy level. Absorption spectra, on the other hand, refer to the range of electromagnetic radiation absorbed by an atom when it transitions from a lower energy level to a higher energy level.
b)
(i) The energy of the photon can be calculated using the equation E = hf, where E is energy, h is Planck's constant, and f is frequency. Thus, E = (6.6 x 10^-34 J s) x (3.0 x 10^8 Hz) / (3 - 1) = 4.4 x 10^-19 J.
(ii) The frequency of the photon is given by f = c / λ, where c is the speed of light and λ is the wavelength. Thus, f = (3.0 x 10^8 m/s) / (6.56 x 10^-7 m) = 4.58 x 10^14 Hz.
(iii) The wavelength of the photon can be calculated using the equation λ = c / f. Thus, λ = (3.0 x 10^8 m/s) / (4.58 x 10^14 Hz) = 6.56 x 10^-7 m.
c)
(i) Soft x-rays have lower energy and longer wavelength than hard x-rays. They are more easily absorbed by matter and are used in medical imaging. Hard x-rays, on the other hand, have higher energy and shorter wavelength and can penetrate denser materials, such as bone and metal.
(ii) The circuit symbol for a p-n junction diode is a triangle with a line at the base. The triangle represents the p-type material, and the line represents the n-type material.
(iii) Doping a semiconductor material involves intentionally adding impurities to change its electrical properties. This is done to create p-type or n-type semiconductors, which have different electron arrangements and conductivities. P-type semiconductors have an excess of holes and are created by doping with elements that have fewer valence electrons, while n-type semiconductors have an excess of electrons and are created by doping with elements that have more valence electrons.
Awọn alaye Idahun
a)
(i) Atomic spectra refers to the range of electromagnetic radiation emitted or absorbed by atoms. It is a characteristic of the arrangement of electrons in atoms and the energy changes that occur within them.
(ii) Emission spectra refer to the range of electromagnetic radiation emitted by an atom when it transitions from a higher energy level to a lower energy level. Absorption spectra, on the other hand, refer to the range of electromagnetic radiation absorbed by an atom when it transitions from a lower energy level to a higher energy level.
b)
(i) The energy of the photon can be calculated using the equation E = hf, where E is energy, h is Planck's constant, and f is frequency. Thus, E = (6.6 x 10^-34 J s) x (3.0 x 10^8 Hz) / (3 - 1) = 4.4 x 10^-19 J.
(ii) The frequency of the photon is given by f = c / λ, where c is the speed of light and λ is the wavelength. Thus, f = (3.0 x 10^8 m/s) / (6.56 x 10^-7 m) = 4.58 x 10^14 Hz.
(iii) The wavelength of the photon can be calculated using the equation λ = c / f. Thus, λ = (3.0 x 10^8 m/s) / (4.58 x 10^14 Hz) = 6.56 x 10^-7 m.
c)
(i) Soft x-rays have lower energy and longer wavelength than hard x-rays. They are more easily absorbed by matter and are used in medical imaging. Hard x-rays, on the other hand, have higher energy and shorter wavelength and can penetrate denser materials, such as bone and metal.
(ii) The circuit symbol for a p-n junction diode is a triangle with a line at the base. The triangle represents the p-type material, and the line represents the n-type material.
(iii) Doping a semiconductor material involves intentionally adding impurities to change its electrical properties. This is done to create p-type or n-type semiconductors, which have different electron arrangements and conductivities. P-type semiconductors have an excess of holes and are created by doping with elements that have fewer valence electrons, while n-type semiconductors have an excess of electrons and are created by doping with elements that have more valence electrons.
Ibeere 61 Ìròyìn
(a) (i) State Newton’s Law of Universal Gravitation.
(ii) Define gravitational field.
(b) (i) Derive the equation relating the universal gravitational constant, G, and the acceleration of free fall, g, at the surface of the earth from Newton’s law of universal gravitation.
(ii) State two assumptions for which the relationship in 8(b)(i) holds.
(c) Calculate the force of attraction between a star of mass 2.00 x 1030 kg and the earth assuming the star is located 1.50 x 108 km from the earth. [Mass of the earth = 5.98 x 1024kg; G = 6.67 x 10-11N m\(^{2}\) kg-2; g = 10 m s\(^{-2}\)
(d) (i) Define escape velocity.
(ii) State two differences between the acceleration of free fall (g) and the universal gravitational constant (G).
a)
-
(i) Newton's Law of Universal Gravitation states that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The force is along the line joining the particles and is given by F = G(m1m2)/r^2, where F is the force of attraction between the particles, m1 and m2 are the masses of the particles, r is the distance between them, and G is the universal gravitational constant.
-
(ii) Gravitational field is a region in space where a mass experiences a force due to the presence of another mass. The gravitational field strength at a point is the force per unit mass experienced by a small test mass placed at that point. It is given by g = F/m, where F is the force experienced by the test mass and m is the mass of the test mass.
b)
-
(i) At the surface of the Earth, the gravitational field strength is equal to the acceleration of free fall (g). Therefore, we have g = GMe/R^2, where Me is the mass of the Earth, R is the radius of the Earth, and G is the universal gravitational constant.
-
(ii) The relationship in 8(b)(i) holds under the assumptions that the Earth is a perfect sphere and has a uniform density distribution.
c)
Using the formula F = G(m1m2)/r^2, where m1 is the mass of the star, m2 is the mass of the Earth, r is the distance between them, and G is the universal gravitational constant, we have:
F = (6.67 x 10^-11 N m^2/kg^2) x (2.00 x 10^30 kg) x (5.98 x 10^24 kg) / (1.50 x 10^11 m)^2
F = 3.52 x 10^22 N
d)
-
(i) Escape velocity is the minimum velocity required by an object to escape the gravitational field of a planet or a star.
-
(ii) The acceleration of free fall (g) depends on the mass and distance of the object experiencing the gravitational force, while the universal gravitational constant (G) is a constant of nature that does not depend on the objects involved. Also, g is a measure of the strength of the gravitational field at a particular point, while G is a measure of the strength of the gravitational force between two objects separated by a distance.
Awọn alaye Idahun
a)
-
(i) Newton's Law of Universal Gravitation states that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The force is along the line joining the particles and is given by F = G(m1m2)/r^2, where F is the force of attraction between the particles, m1 and m2 are the masses of the particles, r is the distance between them, and G is the universal gravitational constant.
-
(ii) Gravitational field is a region in space where a mass experiences a force due to the presence of another mass. The gravitational field strength at a point is the force per unit mass experienced by a small test mass placed at that point. It is given by g = F/m, where F is the force experienced by the test mass and m is the mass of the test mass.
b)
-
(i) At the surface of the Earth, the gravitational field strength is equal to the acceleration of free fall (g). Therefore, we have g = GMe/R^2, where Me is the mass of the Earth, R is the radius of the Earth, and G is the universal gravitational constant.
-
(ii) The relationship in 8(b)(i) holds under the assumptions that the Earth is a perfect sphere and has a uniform density distribution.
c)
Using the formula F = G(m1m2)/r^2, where m1 is the mass of the star, m2 is the mass of the Earth, r is the distance between them, and G is the universal gravitational constant, we have:
F = (6.67 x 10^-11 N m^2/kg^2) x (2.00 x 10^30 kg) x (5.98 x 10^24 kg) / (1.50 x 10^11 m)^2
F = 3.52 x 10^22 N
d)
-
(i) Escape velocity is the minimum velocity required by an object to escape the gravitational field of a planet or a star.
-
(ii) The acceleration of free fall (g) depends on the mass and distance of the object experiencing the gravitational force, while the universal gravitational constant (G) is a constant of nature that does not depend on the objects involved. Also, g is a measure of the strength of the gravitational field at a particular point, while G is a measure of the strength of the gravitational force between two objects separated by a distance.